Дистанційна освіта з інформатики 17.05.2021-22.09.2021

 

Дистанційна освіта з інформатики за травень 2021 року

в період

17.05.2021-22.09.2021

Теоретична частина

Створення та аналіз математичної моделі  табулювання деяких видів функцій з параметром для "коректного" опрацювання  в алгоритмі табулювання функцій із відомими властивостями.

Повторення вивченого матеріалу

Класифікація алгоритмів 

в компетентнісних завданнях 

з теми «Алгоритми та програмування»

 

Під час розв’язування компетентнісних задачах з інформатики створюються, реалізуються, тестуються  найчастіше використовуються:

·        алгоритми форматування(редагування) об’єктів за даними параметрами;

·        алгоритми переміщення(розміщення) об’єктів за даними параметрами;

·        алгоритми видалення(приховування) об’єктів за даними параметрами;

·        алгоритми перевірки властивостей об’єктів за даними параметрами;

·        алгоритми  зміни або заміни властивостей об’єктів за даними параметрами;

·        обчислювальні алгоритми: алгоритми-калькулятори;

·        алгоритми пошуку  об’єктів за даними параметрами;.

·        алгоритми фільтрування змінних величин у лінійному масиві;

·        алгоритми (створення)генерування об’єктів: алгоритми-генератори; 

·        алгоритми перестановки та впорядкування числових та символьних  величин.

 

 В ході розв’язування компетентнісних задач  з інформатики на початкових етапах розв’язування проводиться аналіз властивостей об’єктів та даних умови для того, щоб використати уміння та навички під час реалізації різних видів алгоритмів, а саме створюються:

1.Нелінійні алгоритми:

1.1.                    Алгоритми розгалуження :

1.1.1.  Алгоритми з повним розгалуженням;

1.1.2.  Алгоритми з певним розгалуження;

1.2.   Алгоритми з узагальненим вибором:

1.2.1.  Алгоритми з повним узагальненим вибором;

1.2.2.    Алгоритми з неповним узагальненим вибором;

     1.3 . Циклічні алгоритми:

               1.3.1   Циклічні алгоритми  з лічильником з кроком +1;

               1.3.2   Циклічні алгоритми з лічильником з кроком -1;

               1.3.3   Циклічні алгоритми з лічильником з кроком +m;

               1.3.4    Циклічні алгоритми з лічильником з кроком –m;

       1.4.   Циклічні алгоритми з передумовою:

                1.4.1.   Циклічні алгоритми з простою передумовою;

                1.4.2.   Циклічні алгоритми з складеною  передумовою;

       1.5.  Циклічні алгоритми з післяумовою:

                  1.5.1.   Циклічні алгоритми з простою післяумовою;

                  1.5.2.  Циклічні алгоритми з складеною  післяумовою.

1.6.  Вкладені циклічні алгоритми:

                  1.6.1.   Цикл лічильником має цикл з післяумовою;

                  1.6.2.   Цикл лічильником має цикл з передумовою;

                  1.6.3.   Цикл лічильником має цикл з лічильником;

                  1.6.4.  Цикл передумовою має цикл з лічильником;

                  1.6.5.  Цикл передумовою має цикл з передумовою;

                  1.6.6.  Цикл передумовою має цикл з лічильником;

                  1.6.7.  Цикл ісляумовою має цикл з лічильником;

                  1.6.8.  Цикл післяумовою має цикл з передумовою;

                  1.6.9.  Цикл післяумовою має цикл з післяумовою.

1.7.  Рекурсивні алгоритми:

                    1.7.1.  Алгоритм з рекурсивною процедурою;

                    1.7.2.  Алгоритм з рекурсивною функцією;

1.8.  Ітераційні алгоритми без рекурсії:

                    1.7.1.  Алгоритм з процедурною ітерацією без рекурсії;

                    1.7.2.  Алгоритм з ітераційною функцією без рекурсії;

 

Завдання для самостійного  опрацювання.

 

Приклад  1. Рекурсивний алгоритм факторіалу невід’ємного числа.

Побудуємо математичну модель рекурсивного алгоритму факторіалу невід’ємного числа.

Означення. Факторіалом цілого невід'ємного числа m  називається добуток всіх натуральних чисел від 1 до m і позначається m!.

Приклади: 3!=1*2*3=6;   4!=1*2*3*4=24; 6!= 1*2*3*4*5*6=720.

 

Якщо створити функцію: q(m) = m!, то мають місце рекурентні співвідношення:

k! = k*q(k – 1)       (*)

q(0) = 1           (**)

Перша рівність описує крок рекурсії - метод обчислення q(k) через q(k - 1). Друга рівність вказує, коли при обчисленні функції слід зупинитися. Якщо його не використовувати, то функція буде працювати нескінченно довго.

Наприклад, значення q(7) можна обчислити таким чином:

7! = 7 * q(6) = …= 7 * 6 * 5 * q(4) = 7 * 6 * 5 * 4 * q(3) =

= 7 *6* 5 * 4 * 3 * q(2) = 7 * 6 * 5 * 4 * 3 * 2 * q(1) =

= 7 * 6 * 5 * 4 * 3 * 2 * 1 * 1 = 7*720 = 5040

Очевидно, що при обчисленні q(k) слід зробити k  рекурсивних викликів.

Завдання 1. Самостійно реалізувати та протестувати цей рекурсивний алгоритм мовою програмування.

 

 

Приклад  2. Рекурсивний алгоритм піднесення до степеня числа.

Побудуємо математичну модель рекурсивного алгоритму піднесення до степеня числа.

Найпростішим та досить важливими для інформатики є числа, які є степенями 2. Отже, розглянемо на прикладі таких чисел рекурсивний алгоритм піднесення числа до степеня, який пізніше спробуємо реалізувати ітераційним методом.

Означення. Добуток р*р*р*……*р*р декількох однакових дійсних множників р  називають степенем дійсного числа р, і записють степінь числа р^m.

Приклад. 4³=4*4*4=64;  0,3⁶=0,3*0,3*0,3*0,3*0,3*0,3=0,000729

Для того щоб можливо було написати рекурсивну функцію необхідно виділити основні рекурентні співвідношення. Ми знаємо, що 4⁰ = 1 та 4¹ = 4. Кожна наступна степінь 4 утворюється за принципом множення на 4 числа, що утворилося раніше. Отже, справедливими будуть такі формули:

R(0) = 1,

R(1) = 4,

R(k) = 4 * R(k - 1).

Завдання 3. Самостійно реалізувати та протестувати цей рекурсивний алгоритм мовою програмування.

 

 

Приклад  3. Рекурсивний алгоритм суми цифр цілого невід’ємного числа.

Побудуємо математичну модель рекурсивного алгоритму суми цифр цілого невід’ємного числа.

Означення. Сумою цифр  s(m)=m₁+m₂+m₃+…+ m_k

цілого невід'ємного числа m= m₁m₂m₃…+m_k 

називається сума усіх розрядів цілого невід'ємного числа  і позначається s(m)

Приклади: s(123)=1+2+3=6;   s(1234)=1+2+3+4=10;

s(123456) = 1+2+3+4+5+6=21.

Суму чисел натурального числа k можна знайти за допомогою функції s(k), визначеної в такий спосіб:

s(0) = 0   (*)

s(k) =k mod 10 + s(k div 10)   (**)

Умова продовження рекурсії: сума цифр числа дорівнює останній цифрі плюс сума цифр числа без останньої цифри (числа, поділеної без остачі на 10).

Умова закінчення рекурсії: Якщо число дорівнює 0, то сума його цифр дорівнює 0.

Наприклад, сума цифр числа 576  буде обчислюватися так:

s(576) = 6 + s(57) = 6 + 7 +s (5) = 6 + 7 + 5 + s(0) = 6 + 7 + 5 + 0 = 18.

Завдання 3. Самостійно реалізувати та протестувати цей рекурсивний алгоритм мовою програмування.

 

 

Приклад 4. Відбір в розвідку [ACM, 1999]. Із  n солдатів, вишикуваних в шеренгу, потрібно відібрати кількох в розвідку. Для здійснення цього виконується наступна операція: якщо солдат в шерензі більше ніж 3, то видаляються всі солдати, які стоять на парних позиціях, або всі солдати, які стоять на непарних позиціях. Ця процедура повторюється до тих пір, поки в шерензі залишиться 3 або менше солдатів. Їх і відсилають в розвідку. Обчислити кількість способів, якими таким чином можуть бути сформовані групи розвідників рівно з трьох осіб.

Вхідні дані. Кількість солдатів в шерензі n (0 <k ≤ 10⁵).

Вихідні дані. Кількість способів, якими можна відібрати солдат в розвідку описаним вище способом.

Приклад вхідних та вихідних даних:

Введення      Виведення

10                       2

4                         0

Математична модель рекурсивного алгоритму відбору розвідників.  

Нехай функція r(m) кількість способів, якими можна сформувати групи розвідників з m осіб в шерензі. Оскільки нас цікавлять тільки групи по три розвідника, то r(1) = 0, r(2) = 0, r(3) = 1. Тобто з трьох осіб можна сформувати тільки одну групу, з одного або двох - жодної.

   Якщо  m – парне число, то застосовуючи дану процедуру видалення солдат в шерензі, ми отримаємо або 0,5m солдатів, що стоять на парних позиціях, або  0,5m  солдатів, що стоять на непарних позиціях. Тобто r(m) = 2 · r(0,5m) при парному m.

   Якщо n непарне, то після видалення залишиться або 0,5m солдатів стояли на парних позиціях, або 0,5m + 1 солдат, які стояли на непарних позиціях. Загальна кількість способів при непарному  m  рівне

r(m) = r(m/2) + r(m/2 + 1).

   Таким чином, отримана рекурентна формула для обчислення значення r(n):

r(m) = 2 · r(m / 2), якщо m  - парне =2k;

r (m) = r (m / 2) + r(m/ 2 + 1), якщо m -  непарне =2k-1;

r (1) = 0,  r(2) = 0,   r (3) = 1.

 

Завдання 4. Самостійно реалізувати та протестувати цей рекурсивний алгоритм мовою програмування.

Фронтальне опитування

1.              Яке походження терміна «алгоритм»?

2.              Що ми розуміємо під поняттям «алгоритм»?

3.              Що таке допустимі команди виконавця?

4.              Які є способи опису алгоритмів?

5.              Які властивості повинен мати алгоритм?

6.              Що означає скінченність (дискретність) алгоритму?

7.              Що таке формальність алгоритму?

8.              Що означає масовість алгоритму?

 

Приклад 5. Рекурсивний алгоритм сортування лінійного масиву чисел з процедурою

Завдання. Реалізувати і протестувати алгоритм сортування мовою Паскаль лінійного масиву на 10 цілих чисел.

Program SORT;

var a: array [1..10] of integer; {Масив елементів}

    n: integer;

procedure QuickSort (L, R: Integer); {Швидке сортування масиву A []}

var i, j, x, s, y: integer;

begin    i:=l; j:=r;    x:=a[(l+r) div 2];

  repeat

      while (A[i]<x) do i:=i+1;

      while (x<A[j]) do j:=j-1;

       if (i<=j) then

       begin

      y:=A[i]; a[i]:=a[j]; a[j]:=y;

      i:=i+1; j:=j-1;

    end;

  until (i>j);

  if (l<j) then QuickSort (l, j);

  if (i<r) then QuickSort (i, r);

end;

begin

     writeln ( 'введіть 10 елементів масиву:');

     for n:=1 to 10 do a[n]:=random(200)-random(300);

    { for n:=1 to 10 do readln (a[n]);}

     QuickSort (1, 10); {На вході: ліва і права межа сортування}

     writeln ( 'після сортування:');

     for n:=1 to 10 do write(a[n], '        ' ‘);

end.

 

 

 

 

 

Практична частина

Практична частина

 

Табулювання функцій y(x) різних видів, що задана формулою,   на числовому проміжку хє[a;b]  - це знаходження числових значень функції з наперед відомою точністю і запис її  у вигляді числової  таблиці.

Реалізація табуляції функцій мовою програмування Python3  в середовищі програмування Thonny.

 

Завдання 1.  Створити та реалізувати алгоритм табуляції функцій мовою програмування Python3  в середовищі програмування Thonny  лінійної функції y(x)=kx+m  на числовому проміжку [a;b]  з кроком delta.

У алгоритмі числа(параметри): a; b; k; m; delta - можна змінювати за бажанням користувача.

Проаналізувати основні характеристики лінійної функції: зростання чи спадання, координати точок  перетину з осями координат, місце розташування прямокутного  трикутника, що утворений прямою та осями координат, в координатних чвертях, площа та сторони трикутника, координати центру мас утвореного трикутника.

Реалізація.

 

print('В програмі створена та використана допоміжна функція tabuljacia з циклом з передумовою')

a=-1; b=1; k=-3; m=5; delta=0.5

print('Табуляція лінійної функції вигляду:  у=',k,'*x+',m)

print('Табуляція лінійної функції  на інтервалі:[',a,';',b,']')

print('Крок delta=', delta,'табуляції лінійної функції  на інтервалі:[',a,';',b,']')

def tabuljacia(a,b,k,m):

    x = a; n=0

    while (x>=a)and(x<=b)==1:

        n+=1

        y=round(k*x+m,5)

        print('x',n,'=',x, ";   ", 'y',n,'(',x,')=',k,'*',x,'+',m,'=',y , 'або координати точки прямої:(',x,';',y,')')

        x=x+round(delta,3)

tabuljacia(a,b,k,m)

print('Отримано ', int(1+(b-a)/delta), 'кроків(точок прямої) табуляції лінійної функції  на інтервалі:[',a,';',b,']')

print('********************************')

print('Основні характеристики лінійної функції вигляду:  у=',k,'*x+',m)

if k>0:

    print('Монотонно зростає лінійна функція вигляду:  у=',k,'*x+',m)

if k<0:

    print('Монотонно спадає лінійна функція вигляду:  у=',k,'*x+',m)

if k==0:

    print('Постійна(константа) лінійна функція вигляду:  у=',k,'*x+',m)

print('********************************')

print('Точки перетину з осями координат:')

print('Перетинає вісь Ох(абсцис) лінійна функція вигляду:  у=',k,'*x+',m, ' в точці:(',-k/m,'; 0)')

print('Перетинає вісь Оy(ординат) лінійна функція вигляду:  у=',k,'*x+',m, ' в точці:(0',m,')')

print('********************************')

print('Пряма утворює з осями координат прямокутний трикутник:')

print('Координати  вершин прямокутного трикутника:')

print('Координати  1-ої вершини прямого кута трикутника:О(0;0)')

print('Координати  2-ої вершини трикутника, що належить осі Ох:А(',-k/m,'; 0)')

print('Координати  3-ої вершини трикутника, що належить осі Оу:В(0;',m,')')

if (k<0)and(m>0):

    print('Прямокутний трикутник, кут АОВ=90 град, розташований в 1-ій коорд. чверті')

if (k>0)and(m>0):

    print('Прямокутний трикутник, кут АОВ=90 град, розташований в 2-ій коорд. чверті')

if (k<0)and(m<0):

    print('Прямокутний трикутник, кут АОВ=90 град, розташований в 3-ій коорд. чверті')

if (k>0)and(m<0):

    print('Прямокутний трикутник, кут АОВ=90 град, розташований в 4-ій коорд. чверті')

S=0.5*abs(m)*abs(-k/m); AB=((abs(m))**2+(abs(-k/m))**2)**0.5

print('Площа прямокутного трикутника: S=',0.5*abs(m)*abs(-k/m))

print('Гіпотенуза прямокутного трикутника АОВ: АВ=',((abs(m))**2+(abs(-k/m))**2)**0.5)

print('Катет прямокутного трикутника АОВ на осі абсцис: АО=', abs(-k/m))

print('Катет прямокутного трикутника АОВ на осі абсцис: BО=', abs(m))

print('Найменша висота прямокутного трикутника: Hmin=',2*S/AB)

print('Координати  центру мас трикутника АОВ в точці М(',-k/(3*m),';',m/3,')')

print('Координати  центру кола, описаного навколо трикутника АОВ, в точці Р(',-k/(2*m),';',m/2,')')

print('Довжина найменшої медіани ОР трикутника АОВ:',AB/2,')')

print('Довжина радіусу кола, описаного навколо трикутника АОВ, з центром в точці Р',AB/2,')')

 

Протестувати алгоритм декілька разів.

Тест 1. Якщо a=-2; b=2; k=3; m=5.5; delta=0.25;

Тест 2. Якщо a=-1.25; b=5; k=4; m=8; delta=1;

Тест 3. Якщо a=-25; b=50; k=2; m=8; delta=10;

Тест 4. Самостійно знайдіть  і збільшіть точність обчислення табуляції. (Підказка. У даному алгоритимі за точність обчислення відповідає оператор round(*,*) в допоміжній процедурі tabuljacia, де червона зірочка вказує на кількість знаків після коми у розрахованому числі).

 

Завдання 2.  Створити та реалізувати алгоритм табуляції функцій мовою програмування Python3  в середовищі програмування Thonny  квадратичної функції

 y(x)=kx²+nx+m 

на числовому проміжку [a;b] з кроком delta.

У алгоритмі числа(параметри) a; b; k; n; m; delta - можна змінювати за бажанням користувача.

 

Реалізація.

 

print('В програмі створена та використана допоміжна функція tabuljacia з циклом з передумовою')

a=-25; b=50; k=1; n=2; m=1; delta=10

print('Табуляція квадратичної функції вигляду:  у=',k,'*x^2+',n,'x+',m)

print('Табуляція квадратичної функції  на інтервалі:[',a,';',b,']')

print('Крок delta=', delta,'табуляції квадратичної функції  на інтервалі:[',a,';',b,']')

def tabuljacia(a,b,k,n,m,delta):

    x = a; q=0

    while (x>=a)and(x<=b)==1:

        q+=1; х=round(1*x,5)

        y=round(k*x*x+n*x+m,5)

        print('x',q,'=',x, ";   ", 'y',q,'(',x,')=',k,'*',x,'^2+',n,'*',x,'+',m,'=',y , 'або координати точки параболи:(',x,';',y,')')

        x=x+round(delta,3)

if k!=0:

    tabuljacia(a,b,k,n,m,delta)

    print('Отримано ', int(1+(b-a)/delta), 'кроків(точок параболи) табуляції квадратичної функції  на інтервалі:[',a,';',b,']')

else: print('Це не квадратична функція, бо k=0')

 

Протестувати алгоритм декілька разів.

Тест 1. Якщо a=-100; b=150; k=-3; n=4; m=1; delta=25;

Тест 2. Якщо a=-20; b=50; k=-5; n=40; m=-25; delta=5;

Тест 3. Якщо a=-220; b=300; k=-5; n=40; m=-25; delta=25;

 

 

Завдання 3.  Створити та реалізувати алгоритм табуляції функцій мовою програмування Python3  в середовищі програмування Thonny  дробово-раціональної функції

 y(x)= ^(kх+n) / _{(lx+m )}

на числовому проміжку [a;b] з кроком delta.

У алгоритмі числа(параметри):  a; b; k; n; l; m; delta - можна змінювати за бажанням користувача.

 

Реалізація.

 

 

print('В програмі створена та використана допоміжна функція tabuljacia з циклом з передумовою')

a=-20; b=30; k=2; n=4; l=8; m=-2; delta=3

print('Табуляція дробово-раціональної функції вигляду:  у=(',k,'*x+',n,')/(',l,'*x+',m)

print('Табуляція дробово-раціональної функції  на інтервалі:[',a,';',b,']')

print('Крок delta=', delta,'табуляції дробово-раціональної функції  на інтервалі:[',a,';',b,']')

def tabuljacia(a,b,k,n,l,m,delta):

    x = a; q=0

    while (x>=a)and(x<=b)==1:

        q+=1; х=round(1*x,5)

        y=round((k*x+n)/(l*x+m),5)

        print('x',q,'=',x, "   ", 'y',q,'(',x,')=(',k,'*',x,'+',n,')/(',l,'*',x,'+',m,')=',y , 'або координати точки гіперболи:(',x,';',y,')')

        x=x+round(delta,3)

tabuljacia(a,b,k,n,l,m,delta)

print('Отримано ', int(1+(b-a)/delta), 'кроків(точок гіперболи) табуляції дробово-раціональної функції  на інтервалі:[',a,';',b,']')

if l!=0:

   print('Не має змісту ця дробово-раціональна функція в значенні аргумента х=',-m/l)

 

Протестувати алгоритм декілька разів.

Тест 1. Якщо a=-20; b=30; k=-5; n=4; l=-8; m=-2; delta=5;

Тест 2. Якщо a=-8; b=10; k=0; n=4; l=0; m=-2; delta=4

Тест 3. Якщо  a=-5; b=5; k=2; n=4; l=3; m=-5; delta=1

 

 

Завдання 4.  Створити та реалізувати алгоритм табуляції функцій мовою програмування Python3  в середовищі програмування Thonny  кубічної функції

 y(x)=kx³+ lx² +nx+m 

на числовому проміжку [a;b] з кроком delta.

У алгоритмі числа(параметри) a; b; k; n; m; delta - можна змінювати за бажанням користувача.

 

Реалізація.

 

print('В програмі створена та використана допоміжна функція tabuljacia з циклом з передумовою')

a=-15; b=15; k=1; l=3; n=3; m=1; delta=10

print('Табуляція кубічної функції вигляду:  у=',k,'*x^3+',l,'*x^2+',n,'x+',m)

print('Табуляція кубічної функції  на інтервалі:[',a,';',b,']')

print('Крок delta=', delta,'табуляції кубічної функції  на інтервалі:[',a,';',b,']')

def tabuljacia(a,b,k,l,n,m,delta):

    x = a; q=0

    while (x>=a)and(x<=b)==1:

        q+=1; х=round(1*x,5)

        y=round(k*x*x*x+l*x*x+n*x+m,5)

        print('x',q,'=',x, ";   ", 'y',q,'(',x,')=',k,'*',x,'^3+',l,'*',x,'^2+',n,'*',x,'+',m,'=',y , 'або координати точки кубічної параболи:(',x,';',y,')')

        x=x+round(delta,3)

if k!=0:

    tabuljacia(a,b,k,l,n,m,delta)

    print('Отримано ', int(1+(b-a)/delta), 'кроків(точок параболи) табуляції кубічної функції  на інтервалі:[',a,';',b,']')

else: print('Це не кубічна функція, бо k=0')

 

Протестувати алгоритм декілька разів.

Тест 1. Якщо a =-10; b=10; k=2; l=3; n=3; m=-6; delta=5

Тест 2. Якщо a=-5; b=6; k=-2; l=-5; n=-1; m=-2; delta=2

Тест 3. Якщо a=-100; b=100; k=-1; l=-2; n=-1; m=-1; delta=20

 

Завдання 5.  Створити та реалізувати алгоритм табуляції функцій мовою програмування Python3  в середовищі програмування Thonny функції суми двох модулів лінійних виразів:  y=|kx+n| + |lx+m|  

на числовому проміжку [a;b] з кроком delta.

У алгоритмі числа(параметри) a; b; k; n; m; delta - можна змінювати за бажанням користувача.

 

Реалізація.

print('В програмі створена та використана допоміжна функція tabuljacia з циклом з передумовою')

a=-100; b=100; k=-1; l=-2; n=-1; m=-1; delta=20

print('Табуляція функції суми двох модулів вигляду:  у=|',k,'*x+',l,'|+|',l,'*x+',m,'|')

print('Табуляція кубічної функції  на інтервалі:[',a,';',b,']')

print('Крок delta=', delta,'табуляції функції суми двох модулів на інтервалі:[',a,';',b,']')

def tabuljacia(a,b,k,l,n,m,delta):

    x = a; q=0

    while (x>=a)and(x<=b)==1:

        q+=1; х=round(1*x,5)

        y=round(abs(k*x+n)+ abs(l*x+m),5)

        print('x',q,'=',x, ";   ", 'y',q,'(',x,')=|',k,'*',x,'+',n,'|+|',l,'*',x,'+',m,'|=',y , 'або координати точки ламаної:(',x,';',y,')')

        x=x+round(delta,3)

tabuljacia(a,b,k,l,n,m,delta)

print('Отримано ', int(1+(b-a)/delta), 'кроків(точок параболи) табуляції функції суми двох модулів  на інтервалі:[',a,';',b,']')

 

Протестувати алгоритм декілька разів.

Тест 1. Якщо a =-12; b=10; k=2; l=3; n=3; m=-6; delta=3

Тест 2. Якщо a=-7; b=6; k=-2; l=-5; n=-1; m=-2; delta=1

Тест 3. Якщо a=-102; b=92; k=-1; l=-2; n=-1; m=-1; delta=25

 

Завдання 6.  Створити та реалізувати алгоритм розв’язування квадратного рівняння мовою програмування Python3  в середовищі програмування Thonny функції суми двох модулів лінійних виразів:  q*x*x+g*x+h=0  на множині дійсних чисел, де х- невідоме дійсне число.

У алгоритмі числа(параметри) q; g; h - можна змінювати за бажанням користувача.

 

Реалізація. У алгоритмі використано розгалуження.

print('Алгоритм розв’язування квадратного рівняння: q*x*x+g*x+h=0')

q=1; g=2; h=1

D=g*g-4*q*h; print('Дискримінант D=',D)

if g*g-4*q*h>0:

    w1=(-g-( g*g-4*q*h)**0.5)/(2*q)

    w2=(-g+( g*g-4*q*h)**0.5)/(2*q)

    print('Два корені у квадратного рівняння:')

    print('х1= ',w1, '; x2=',w2)

elif g*g-4*q*h==0:

     v1=-g/(2*q)

     print('Два корені рівні між собою у квадратного рівняння:')

     print('х1=x2=',v1)

elif g*g-4*q*h<0:

     print('Дійсних коренів немає у квадратного рівняння')

 

Протестувати алгоритм декілька разів.

Тест 1. Якщо q=4; g=-4; h=1

Тест 2. Якщо q=6; g=8; h=-1

Тест 3. Якщо q=3; g=2; h=10

 

 

 

Результат виконаної практичної роботи це файли( із результатами виконання програм) надіслати вашому учителю на електронну скриньку: 
vinnser@gmail.com (Сергій Петрович)
ktdfz@i.ua (Юрій Васильович)

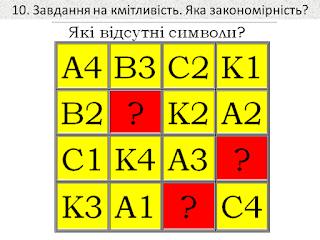
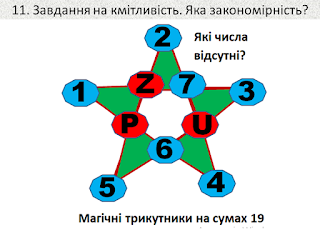
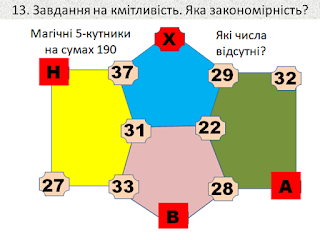
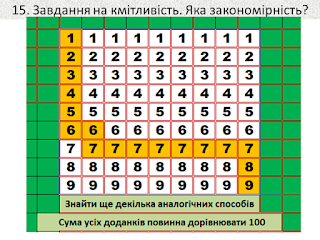
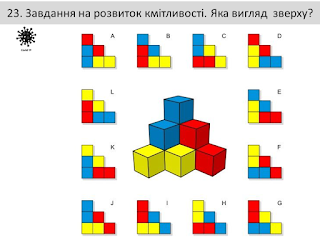
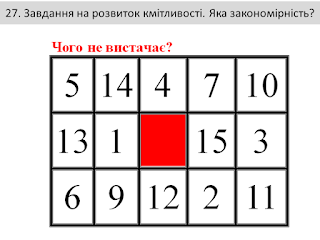
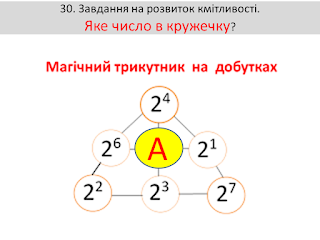
Завдання на розвиток кмітливості