Система числення

Сукупність прийомів та правил найменування й позначення чисел називається системою числення.

 Звичайною для нас і загальноприйнятою є позиційна десяткова система числення. Як умовні знаки для запису чисел вживаються цифри.

Система числення, в якій значення кожної цифри в довільному місці послідовності цифр, яка означає запис числа, не змінюється, називається непозиційною. Система числення, в якій значення кожної цифри залежить від місця в послідовності цифр у записі числа, називається позиційною.

Щоб визначити число, недостатньо знати тип і алфавіт системи числення. Для цього необхідно ще додати правила, які дають змогу за значеннями цифр встановити значення числа.

Найпростішим способом запису натурального числа є зображення його за допомогою відповідної кількості паличок або рисочок. Таким способом можна користуватися для невеликих чисел.

Наступним кроком було винайдення спеціальних символів (цифр). У непозиційній системі кожен знак у запису незалежно від місця означає одне й те саме число. Добре відомим прикладом непозиційної системи числення є римська система, в якій роль цифр відіграють букви алфавіту: І - один, V - п'ять, Х - десять, С - сто, Z - п'ятдесят, D -п'ятсот, М - тисяча. Наприклад, 324 = СССХХІV. У непозиційній системі числення незручно й складно виконувати арифметичні операції.

Загальновживана форма запису числа є насправді не що інше, як скорочена форма запису розкладу за степенями основи системи числення, наприклад

130678=1*10⁵+3*10⁴+0*10³+6*10²+7*10¹+8

Тут 10 є основою системи числення, а показник степеня - це номер позиції цифри в записі числа (нумерація ведеться зліва на право, починаючи з нуля). Арифметичні операції у цій системі виконують за правилами, запропонованими ще в середньовіччі. Наприклад, додаючи два багатозначних числа, застосовуємо правило додавання стовпчиком. При цьому все зводиться до додавання однозначних чисел, для яких необхідним є знання таблиці додавання.

Проблема вибору системи числення для подання чисел у пам'яті комп'ютера має велике практичне значення. В разі її вибору звичайно враховуються такі вимоги, як надійність подання чисел при використанні фізичних елементів, економічність (використання таких систем числення, в яких кількість елементів для подання чисел із деякого діапазону була б мінімальною). Для зображення цілих чисел від 1 до 999 у десятковій системі достатньо трьох розрядів, тобто трьох елементів. Оскільки кожен елемент може перебувати в десятьох станах, то загальна кількість станів - 30, у двійковій системі числення 999₁₀=1111100, необхідна кількість станів - 20 (індекс знизу зображення числа - основа системи числення). У такому розумінні є ще більш економічна позиційна система числення - трійкова. Так, для запису цілих чисел від 1 до у десятковій системі числення потрібно 90 станів, у двійковій - 60, у трійковій - 57. Але трійкова система числення не дістала поширення внаслідок труднощів фізичної реалізації.

Cпосіб переходу від 

двійкової системи числення 

до десяткової системи числення:

(100011111)₂=

=1*2⁸+1*2⁷+0*2⁶+0*2⁵+1*2⁴+1*2³+1*2²+1*2¹+1*2⁰=

=256+128+0+0+16 +8+4+2+1=(415)₁₀.

Тому найпоширенішою для подання чисел у пам'яті комп'ютера є двійкова система числення. Для зображення чисел у цій системі необхідно дві цифри: 0 і 1, тобто достатньо двох стійких станів фізичних елементів. Ця система є близькою до оптимальної за економічністю, і крім того, таблички додавання й множення в цій системі елементарні:

+ 0 1 * 0 1 0 0 1 0 0 0 1 1 10 1 0 1

Оскільки 2³=8, а 2⁴=16 , то кожних три двійкових розряди зображення числа утворюють один вісімковий, а кожних чотири двійкових розряди - один шістнадцятковий. Тому для скорочення запису адрес та вмісту оперативної пам'яті комп'ютера використовують шістнадцяткову й вісімкову системи числення. Нижче в таблиці 1 наведені перших 16 натуральних чисел записаних в десятковій, двійковій, вісімковій та шістнадцятковій системах числення.

Таблиця 1

10 2 8 16 0 0000 0 0 1 0001 1 1 2 0010 2 2 3 0011 3 3 4 0100 4 4 5 0101 5 5 6 0110 6 6 7 0111 7 7 8 1000 10 8 9 1001 11 9 10 1010 12 A 11 1011 13 B 12 1100 14 C 13 1101 15 D 14 1110 16 E 15 1111 17 F

Приклад 1 . Системи числення з основою‚ кратною 2:

а) вісімкове число 273‚54 переводиться у двійкову систему (8 = 2³ ) так:

273‚54₈ = (010)(111)(011)‚(101)(100)=10111011‚1011₂ ;

б) двійкове число 11011‚0011 переводиться у вісімкову систему числення так:

1011‚0011₂ = 11(011)‚(001)1 = (011)(011)‚(001)(100) = 33‚14₈ ;

в) шістнадцяткове число A5,B1E переводиться в двійкову систему числення (16 = 2⁴ ) так:

A5,B1E₁₆ = (1010)(0101),(1011)(0001)(1110) = 10100101,10110001111₂

В процесі налагодження програм та в деяких інших ситуаціях у програмуванні актуальною є проблема переведення чисел з однієї позиційної системи числення в іншу. Якщо основа нової системи числення дорівнює деякому степеню старої системи числення, то алгоритм переводу дуже простий: потрібно згрупувати справа наліво розряди в кількості, що дорівнює показнику степеня і замінити цю групу розрядів відповідним символом нової системи числення. Цим алгоритмом зручно користуватися коли потрібно перевести число з двійкової системи числення у вісімкову або шістнадцяткову. Наприклад, 10110₂=10 110=26₈, 1011100₂=1011100=5C₈

у двійковому відбувається за зворотнім правилом: один символ старої системи числення заміняється групою розрядів нової системи числення, в кількості рівній показнику степеня нової системи числення. Наприклад, 472₈=100 111 010=100111010₂, B516=10110101=10110101₂

Як бачимо, якщо основа однієї системи числення дорівнює деякому степеню іншої, то перевід тривіальний. У протилежному випадкові користуються правилами переведення числа з однієї позиційної системи числення в іншу (найчастіше для переведення із двійкової, вісімкової та шістнадцяткової систем числення у десяткову, і навпаки).

1. Для переведення чисел із системи числення з основою p в систему числення з основою q, використовуючи арифметику нової системи числення з основою q, потрібно записати коефіцієнти розкладу, основи степенів і показники степенів у системі з основою q і виконати всі дії в цій самій системі. Очевидно, що це правило зручне при переведенні до десяткової системи числення.

Наприклад:

з вісімкової в десяткову:

735₈=7*10₈²+3*10₈¹+5*10₈⁰= 7*8₁₀²+3*8₁₀¹+5*8₁₀⁰=477₁₀

з двійкової в десяткову:

110100101₂=1*10₂⁸+1*10₂⁷+ 0*10₂⁶+1*10₂⁵+0*10₂⁴+0*10₂³+ 1*10₂²+0*10₂¹+1*10₂⁰= 1*2₁₀⁸+1*2₁₀⁷+0*2₁₀⁶+1*2₁₀⁵+ 0*2₁₀⁴+0*2₁₀³+1*2₁₀²+0*2₁₀¹+ 1*2₁₀⁰=421₁₀

2. Для переведення чисел із системи числення з основою p в систему числення з основою q з використанням арифметики старої системи числення з основою p потрібно:

• для переведення цілої частини:
• послідовно число, записане в системі основою p ділити на основу нової системи числення, виділяючи остачі. Останні записані у зворотному порядку, будуть утворювати число в новій системі числення;
• для переведення дробової частини:
• послідовно дробову частину множити на основу нової системи числення, виділяючи цілі частини, які й будуть утворювати запис дробової частини числа в новій системі числення.

Цим самим правилом зручно користуватися в разі переведення з десяткової системи числення, тому що її арифметика для нас звичніша.

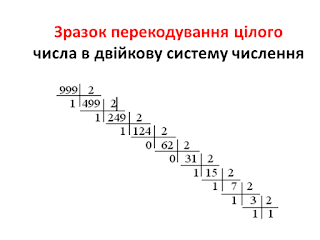
Приклади: 999,35₁₀=1111100111,01011₂

для цілої частини:

Перевід цілої частини числа. Число q записують в p -мі системі числення. Ділять в p -вій системі цілу частину числа на q і отримують остачу‚ яка є останньою цифрою шуканого числа. Отриману частку знову ділять на q і отримують остачу‚ яка є передостанньою цифрою шуканого числа і т.д. процес продовжують до тих пір‚ поки остача не стане меншою ‚ ніж число q . Остання остача буде першою (старшою) цифрою числа.

для дробової частини:

Перевід дробової частини. Число q записують в p -мі системі числення. Дріб множимо в p -вій системі на q . Ціла частина добутку дорівнює першій цифрі запису числа. Дробову частину добутку знову множимо на q . Ціла частина добутку дорівнює наступній цифрі запису числа в системі числення з основою q . Процес продовжують до тих пір поки не отримаємо добуток у вигляді цілого числа або не отримаємо потрібної кількості цифр шуканого дробу.

Переведення чисел ( z)#р→( y)#10

 Відомо, що (125)#10=(7D)#16.

Як же здійснювати перехід з певної системи числення в десяткову і навпаки?

 Для цього необхідно абстрагувати систему числення, яка відмінна від десяткової, тобто подати її в узагальненому вигляді. Такою узагальненою системою є система числення з основою р. Алфавіт такої системи: 0, 1, …, р-1.

Наприклад, основа п’ятіркової системи числення – р=5.

Алфавіт цієї системи: 0, 1, … 5-1, тобто: 0, 1, 2, 3, 4.

Перехід числа з системи з основою числення р в десяткову здійснюється за такою формулою:

( а а а … аaа)#р = (а*р^k + а*р^k-1 + а*р^k-2 + … + a*p^2 + a*p^1 + a*p^0)#10

Раніше ми записали, що (144)#8=(100)#10.

Давайте перевіримо:

(144)#8 = 1*8^2 + 4*8^1 + 4*8^0 = 1*64 + 4*8 + 4*1 = 64+32+4 = (100)#10

Отже, для того, щоб перевести ціле число з системи, що має основу р, в десяткову систему числення, потрібно: 1. Проставити під цифрами даного числа справа наліво номер позиції починаючи з 0. 2. а) цифру найстаршого розряду числа з основою р (нехай це а) записати після знаку дорівнює; б) поставити знак множення; в) записати р; г) над числом р поставити степінь – номер позиції записаної цифри а; д) поставити знак плюс. 3. Виконати пункт 2 для цифри молодшого розряду. 4. Виконувати пункт 2, аж поки не дійдемо до цифри, позиція якої 0. 5. Виконати обчислення, записати число, поставити основу 10.

Задача. Перевести п’ятіркове число (2413)#5 в десяткове.

Розв’язання. (2413)#5=2*5^3+4*5^2+1*5^1+3*5^0=250+100+8=(358)#10

 Задача. Перевести шістнадцяткове число (7D)#16 в десяткове.

Розв’язання. (7D)#16=7*16^1+13*16^0=11^2+13=(125)#10

Завдання для самостійного опрацювання.

Здійснити перехід від однієї системи

числення до іншої системи числення:

1)(1022)₃®(…)₁₀

2)(2013)₄®(…)₁₀

3)(23041)₅®(…)₁₀

4)(2А)₁₆®(…)₁₀

5)(110010)₂®(…)₁₀

6)(15)₆®(…)₁₀

7)(29)₁₀®(…)₂

8) (38)₁₀®(…)₄

9)(401)₁₀®(…)₃

10) (267)₁₀®(…)₅

Задача Per_10_2

   Перевести натуральне число N із 10-ової в 2-ову систему числення.

  Технічні умови. Програма зчитує з клавіатури натуральне число N (N<=103). Програма виводить на екран шукане натуральне число - запис у 2-овій системі числення.

  Приклад
          Введення:   5       
          Виведення:  101

Задача  Per_10_a

   Перевести натуральне число N із 10-ової у систему числення за основою а (2<= a <10).

  Технічні умови. Програма зчитує з клавіатури натуральні числа N (N<=109) і а (2<= a <10). Програма виводить на екран шукане натуральне число - запис у а-овій системі числення.

  Приклад
          Введення:   54  7      
          Виведення:  105

Двійкова система числення. Десяткова система числення.

Задача N2_N10. Переведіть  натуральне число із двійкової системи числення в десяткову систему числення, використовуючи мову Pascal.

Технічні умови.  З клавіатури вводяться  числа із двійкової системи числення, використовуючи цілий тип даних longint. На виході  отримуємо це ж число, що записане у десятковій системі числення.

Приклад.  А)Введення:11₂, виведення:3₁₀;Б) Введення:1010₂, виведення:10₁₀;  В)Введення:1111₂, виведення:15₁₀; Г) Введення:10000₂ , виведення:16₁₀. 

Розв’язання.Кодування мовою програмування Pascal: 

program n2_n10;

var  n10, n2,  ost, k : longint;

begin

write( ‘Введіть натуральне число в двійковій системі  із цифр  1 та  0,   n2=: ');

 read(n2); k:=1;  n10:=0;  while n2 > 0 do

begin

ost:= n2 mod 10;   if  ost=1 then  n10:= ost*k+n10;

n2:= n2 div 10;   k:= k*2; end;

writeln('  Число в десятковій  системі  має запис  n10 = ', n10);

end.

Задача N10_N2. Переведіть  натуральне число із десяткової  системи числення в двійкову систему числення , використовуючи мову Pascal.

Технічні умови.  З клавіатури вводяться  числа в десятковій системи числення, використовуючи цілий тип даних longint. На виході  отримуємо це ж число, що записане у двійковій системі числення.

Приклад.  А)Введення:3₁₀, виведення:11₂; Б)Введення:10₁₀, виведення:1010₂; 

В)Введення:15₁₀, виведення:1111₂; Г) Введення:16₁₀,  виведення:10000₂. 

Розв’язання. Кодування мовою програмування Pascal: 

program n10_n2;

var a, b, n10, n2,  ost, k : longint;

begin

write( ‘Введіть натуральне число в десятковій  системі  числення  із цифр:  1,2,3,4,5,6,7,8,9,0,  n10=  ');

 read (n10);   k:=1; n2:=0;    while n10 > 0 do

begin

        ost:= n10 mod 2;   n10:= n10 div 2;  n2:= ost*k+n2;

        k:= k*10; 

end;

         writeln('   Число в двійковій  системі числення  має запис  n2 = ',n2);

         end.

Контрольні запитання.

1.    Наведіть синтаксис запису циклів з лічильником мовою Pascal?

2.    Наведіть синтаксис запису циклів з передумовою мовою Pascal?

3.    Наведіть синтаксис запису циклів з післяумовою мовою Pascal?

4.    Як записуються  розгалуження мовою Pascal?

5.    Як записуються  складені логічні  умови у форматі  if … then … else..;, що об'єднують декілька простих логічних умов?

6.    Наведіть синтаксис оператора одноальтернативного  розгалуження.

7.    До яких типів даних не може належати значення виразу-селектора в операторі вибору?

8.    У чому полягає відмінність між циклами з передумовою та циклами з післяумовою?

9.    Якому типу даних може належати лічильник у циклі  for?

10.   Яке значення має лічильник після завершення циклу  for?

11.   Що може спричинити «зациклення» програми?

12.   За яких умов цикли while та for не виконаються жодного разу?

13.   Коли цикл виконується лише один раз?

14.   У чому полягає відмінність між такими операторами циклів, як  for...to...do  та for...downto...do?

15.   Яка структура працює ефективніше: вкладені оператори іf ...then...else чи серія операторів іf...then? Відповідь обґрунтуйте.

16.   Як можна пропустити деякі оператори програми, що належать тілу циклу, не видаляючи ці оператори?

17.   Як підвищити ефективність роботи вкладених структур if...then...else?