06.12.2021-12.12.2021
Тема:
Нелінійні
алгоритми.
Теоретична частина
Клітинкові фігури.
Означення клітинкової фігури: Фігурка
називається клітинковою, якщо вона складається з квадратиків розміром 1х1, і
кожен квадратик 1х1 має спільну сторону з неменше ніж одним квадратиком 1х1.
Означення К-клітинкової фігури: К-клітинковою
фігурою називається клітинкова фігура,
що складається з квадратів, розміром 1х1, кількість яких рівна числу
К.
Зауваження. Два квадратики 1х1 не будуть утворювати клітинкові
фігурки, якщо вони мають тільки одну спільну точку з сусіднім квадратом 1х1,
тобто вершину.
Одноклітинкова та
двоклітинкова фігурки це відповідно квадратик 1х1 та прямокутник 1х2.
Триклітинкових фігурок всього є двох видів. Чотириклітинкових фігурок є п’ять видів. П’ятиклітинкових
фігурок всього є 12 видів.
Завдання для вироблення умінь та навичок використовувати
властивості.
- Чи
можна розрізати клітинковий квадрат 5х5 на різні 5-клітинкові фігурки?
а) так завжди можна; б) ні; в) можна тільки в окремих; г) інша відповідь.
Відповідь: так,
завжди можна.
- Яку
найбільшу кількість нерівних клітинкових фігурок можна помістити в квадрат
5х5 без накладань?
а) 5; б) 6; в) 7; г) 8.
Відповідь: вісім.
- Яку
найбільшу кількість нерівних клітинкових
фігурок можна помістити в квадрат 4х4 без накладань?
а) 5; б) 6; в) 7;
г) 8.
Відповідь: п’ять.
- Чи
можна розрізати клітинковий квадрат 4х4 на: а) усі різні; б) рівні 4-клітинкові
фігурки?
а) так завжди можна; б) ні;
в) можна тільки в окремих; г) інша відповідь.
Відповідь: а) так; б)так,
для двох видів.
- Яку
найбільшу кількість 5-клітинкових фігурок можна помістити в квадрат 4х4?
а) 5; б) 6; в) 7;
г) 8.
Відповідь: три.
- Чи
можна розрізати клітинковий квадрат 100х100 на: а) Т-подібні 4-клітинкові
фігурки?
а) так завжди можна; б) ні; в) можна тільки в окремих; г) інша відповідь.
Відповідь: так.
- Складіть
таблицю 5-клітинкових фігурок. Скільки видів таких фігурок?
а) 12; б) 11; в) 13;
г) 10.
Відповідь: 12.
- Розмістіть
найбільшу кількість 5-клітинкових фігурок виду «кутик» у квадраті 5х5?
а) 2; б) 3; в) 4;
г) 5.
Відповідь: чотири.
- Чи
можна розрізати клітинковий квадрат 4х4 на: а) 5 різних клітинкових фігурок
б) 6 різних клітинкових фігурок?
а) так завжди можна; б) ні; в) можна тільки в окремих; г) інша відповідь.
Відповідь: а)так; б)
ні.
Інформаційна частина заняття.
Учень розповідає про
українського математика Михайла Кравчука
"Михайло Кравчук -
математик широкого масштабу. Його ім'я добре відоме у світовій математичній
науці. Світ не знав лише, що він - українець." Довго не знали про цю
надзвичайно талановиту людину і його земляки. Про це з болем пише у своїй
статті його син О.М. Кравчук, доцент Волинського державного університету. Адже
ім'я М. Кравчука було занесено до списку "ворогів народу", а сам він,
повний енергії і творчих задумів, був засланий на Колиму і пішов з життя у
неповних п'ятдесят років.
Лише 1992 року, після довгих
літ забуття, наукова громадськість України та світу широко відзначила 100-річчя
від дня народження видатного вченого. Його ім'я було занесено по лінії ЮНЕСКО
до Міжнародного календаря визначних наукових діячів. Для цього були поважні
підстави, адже праці М.П. Кравчука становлять фундаментальне надбання кількох
галузей математичної науки.
З наведених нарисів та статей
ти довідаєшся, що народився М. Кравчук 1892 року у селі Човниці на Волині в
сім'ї інженера-землеміра. Початкову освіту він здобув удома. Його мати була
освіченою жінкою, знала кілька іноземних мов і добре виховувала чотирьох дітей.
1901 року сім'я переїхала до Луцька, де в 1910 році Михайло Кравчук закінчив
гімназію із золотою медаллю. Цього ж року він вступив на математичне відділення
фізико-математичного факультету університету Св. Володимира в Києві, закінчив
його у 1914 р. з дипломом 1-го ступеня і залишився в ньому працювати.
Відтоді й почалася його титанічна творча наукова і педагогічна праця. Він
викладав різні математичні курси у багатьох вищих та середніх закладах м.
Києва.
У роки громадянської війни М.
Кравчук виїжджає на село. У 1919-21 рр. він був викладачем і директором школи в
селі Саварці на Богуславщині. Його колишні учні, які вступали до технікумів та вузів,
вражали викладачів своїми знаннями з математики. У цій школі під опікою М.П.
Кравчука розпочав свій шлях у велику науку сільський хлопець Архип Люлька,
пізніше - відомий український вчений, творець реактивних авіадвигунів. До речі,
у Київському політехнічному інституті лекції М. Кравчука слухав і майбутній
славетний конструктор космічних кораблів Сергій Корольов.
Михайло Пилипович був людиною
неабиякої ерудиції та культури. У 25 років він став приватдоцентом кафедри
математики, у 33 - доктором наук, у 37 - дійсним членом Всеукраїнської академії
наук. Вільно володіючи кількома мовами, він підтримував наукові й особисті
дружні стосунки з відомими математиками світу - Адамаром, Гільбертом, Курантом
та ін. Свої наукові праці писав різними мовами, але найбільше - рідною.
Академік М. П. Кравчук брав найактивнішу участь у творенні української наукової
термінології та у запровадженні наукової мови в математичну галузь.
М. П. Кравчук належав до тих учених, чиї праці відкривають нові шляхи у
розвитку науки і передбачають напрямки її розвитку в майбутньому.
"Моя любов - Україна і
математика", - ці слова Михайла Пилиповича Кравчука викарбовано на
гранітному постаменті пам'ятника, який встановлено йому в 2003 році перед
корпусом музею Національного технічного університету України "Київський
"Київський політехнічний інститут". У селі, де він народився, в 1979
році відкрито музей та встановлено погруддя великого патріота і математика.
Практична
частина
Завдання 1. Створити
алгоритми мовою програмування Python3 для
знаходження найбільшого спільного дільника
НСД(р; с), найменшого спільного кратного НСК(р; с), для двох натуральних
чисел в середовищі
програмування Thonny.
Реалізація.
import random
print(" Алгоритм 1 для пошуку НСд та НСК")
a=84*random.randint(1,1000000)
b=105*random.randint(1,1000000)
def nsd(x,y):
if x!=0:
return nsd(y%x, x)
else:
return y
def nsk(x,y):
return
(x//nsd(x,y))*y
print("HCD(",a,b,")=",
nsd(a,b))
print("HCK(",a,b,")=", nsk(a,b))
Протестувати алгоритм
для: 1)двоцифрових чисел; 2)
трицифрових чисел; 3) чотирицифрових чисел.
Завдання 2. Створити
алгоритми мовою програмування Python3 для знаходження розв'язків лінійного рівняння в середовищі програмування Thonny.
Реалізація.
import
random
print("
Алгоритм 2 для пошуку коренів лінійного рівняння")
k=10000
a=random.randint(-k,k)
b=random.randint(-k,k)
print("Дано
рівняння: ",a,"*x=",b)
if (a==0)and(b==0):
print("Будь-яке число є коренем рівняння: 0х=0")
if (a==0)and(b!=0):
print("Немає розвязків у цього рівняння:
0х=р")
if
(a!=0)and(b!=0):
print("Один
розвязок: х=", b/a)
Протестувати алгоритм
для: 1)двоцифрових чисел; 2)
трицифрових чисел; 3) чотирицифрових чисел.
Завдання 3. Створити алгоритм мовою
програмування Python3 для
знаходження властивостей
подільності трицифрового натурального числа
в середовищі програмування Thonny.
Реалізація.
import
random
print("
Алгоритм 3 для пошуку властивостей числа: abc")
k=random.randint(100,998)
print("трицифрове число:",k)
a=k//100;
print("цифра розряду сотень:",a)
b=(k-a*100)//10;
print("цифра розряду десятків:",b)
c=k%10;
print("цифра розряду одиниць:",c)
if
(a!=b)and (a!=c)and (b!=c):
print("немає рівних цифр")
if
(a==b) or (b==c) or (a==c):
print("має однакові цифри")
if
(a==c):
print("це число паліндромне")
g=max([a,b,c]);
q=min([a,b,c])
p=a+b+c-g-q
if
q+p>g:
print("це трикутне число")
if
g==p+q:
print("це дивакувате число")
if
g==p*q:
print("це добуткове число")
if
(g==p**2)or(g==q**2)or(p**2==q):
print('це квадратоване число')
if
(g==c)and(a==q)and(p==b):
print('це неспадний порядок цифр числа')
if
(g==a)and(q==c)and(p==b):
print('це незростаючий порядок цифр числа')
if
(c%2==0)and((a+b+c)%3==0)and((a+b+c)%9==0):
print('це парне число, що ділиться на 3, на 6, на 9, на
18')
if
(c%2==0)and(c%5==0)and((a+b+c)%3==0):
print('це парне число, що ділиться на 3, на 6, на 10, на
15')
h=[2,3,5,7,11,13,17,19,23,29,31]
v=['None']*11
z=0
m=0
for
j in range(len(h)):
z=z+k%int(h[j])
print("k=",k,"=",
h[j],"*",k//int(h[j]), "+", k%int(h[j]))
if k%int(h[j])==0:
print("це складене число")
else:
m=m+1
if
m==11:
print("це просте число")
else:
print("це складене число")
Завдання 4. Створити алгоритм мовою програмування Python3 для знаходження найменшого
значення виразу з модулями вигляду: m*|x-a|+n*|x-b|, якщо змінні a,b,m,n – натуральні числа в середовищі програмування Thonny.
Реалізація.
print("
Алгоритм 4 для пошуку найбільшого або найменшого значення виразу")
m=random.randint(-q,q)
n=random.randint(-q,q)
a=random.randint(-q,q)
b=random.randint(-q,q)
print("Вираз:",m,"*|x-",a,"|+",n,"*|x-",b,"|")
print("m=",m,
"n=",n)
print("a=",a,
"b=",b)
print("m+n=",m+n)
FA=n*abs(a-b)
FB=m*abs(b-a)
if m+n>=0:
print(" MIN_F(х)=
m*|x-a|+n*|x-b|=", min([FA,FB]))
else:
print("MAX_F(х)=
m*|x-a|+n*|x-b|=", max([FA,FB]))
Завдання 5. Створити, реалізувати, протестувати алгоритм мовою програмування Python3 в середовищі програмування Thonny для знаходження кількості двоцифрових чисел, сума цифр
яких дорівнює 9.
Математична модель завдання 4: ab=10*a+b i перевiрити умови a+b=9=9+0=8+1=7+2=6+3=5+4
Реалізація.
print('Алгоритм 5 пошуку
кількості двоцифрових чисел з сумою цифр
9')
k=0
for a in
range(1,10):
for b in range(0,10):
if a+b==9:
k=k+1
print('Шукане двоцифрове число з сумою цифр
9', 10*a+b)
print('Kількість двоцифрових чисел з сумою цифр 9 =', k)
Завдання
6. Створити, реалізувати, протестувати алгоритм мовою програмування Python3 в середовищі програмування Thonny для знаходження кількості трицифрових чисел, сума цифр
яких дорівнює 5.
Математична модель завдання 5: abc=100*a+10*b+c i перевiрити умови a+b+c=5=5+0+0=4+1+0=3+2+0=2+2+1=3+1+1
та врахувати перестановки
Реалізація.
print('Алгоритм 6 пошуку кількості 3-цифрових чисел з сумою цифр 5')
k=0
for a in
range(1,10):
for b in range(0,10):
for c in range(0,10):
if a+b+c==5:
k=k+1
print('Шукане 3-цифрове число
з сумою цифр 5 =', 100*a+10*b+c)
print('Kількість 3-цифрових чисел з сумою цифр 5 =', k)
Результати
виконання практичної частини надіслати не eлектронну адресу учителя:
vinnser@gmail.com
**********************
*************
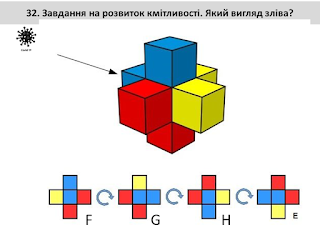
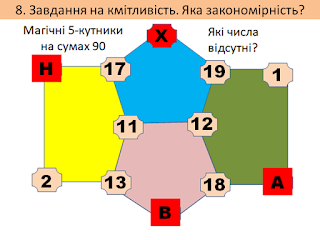
Завдання на розвиток кміливості

































Немає коментарів:
Дописати коментар