7 клас. Інформатика. Дистанційне навчання: січня 2021

Дистанційна освіта з інформатики в період лютого 2021 року

01.02.2021 - 07.02.2021

Конспект уроку для учнів

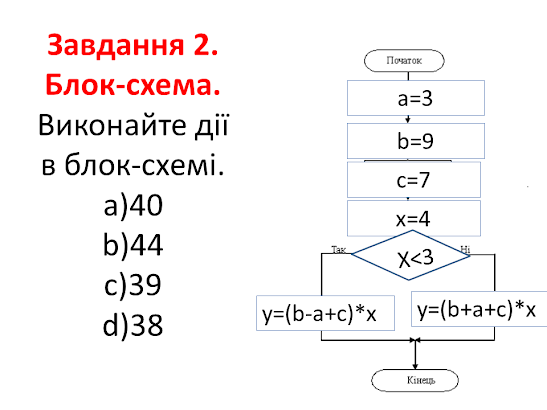
Тема: Вказівка присвоювання. Середовище опису та виконання лінійних та нелінійних алгоритмів Thony мовою програмування Python3.

Теоретична частина. Вікі-підручник Python3

Фізкультхвилинка

Один, два – усі піднялись,

Повернулись, похитались.

Три, чотири – руки вгору,

В сторони і вгору знову.

П’ять, шість – опустили,

І швиденько всі присіли.

Сім, вісім – всі малята

Стрибають, як жабенята.

Дев’ять, десять, - рівно стали

І за парти посідали.

Осмислюємо властивості алгоритмів на текстовому матеріалі різнорівневих компететнісних завдань:

Зразок 1.
Створити алгоритм для складання магічних числових стовпців Вінницького вигляду:
а ... а ... а ... а ... а = 0
а ... а ... а ... а ... а = 1
а ... а ... а ... а ... а = 2
а ... а ... а ... а ... а = 3
а ... а ... а ... а ... а = 4
................
а ... а ... а ... а ... а = n-2
а ... а ... а ... а ... а = n-1
а ... а ... а ... а ... а = n

Де замість знаку «...» можна нічого не ставити а дозволяється поставити будь-яку арифметичну дію: додавання, віднімання, множення, ділення. А також у виразі можна поставити: круглі дужки, квадратні дужки- це ціла частина від дробового числа, фігурні дужки - це дробова частина від будь-якого числа, можна поставити квадратний корінь, можна поставити дію факторіал числа.

Реалізація.
Алгоритм матиме такі команди:
(а -а)*а*а*а = 0
а:а+(а-а)*а =1
(а+а):а+а-а=2
(а+а):а+а:а=3
(а+а+а+а):а=4
.............
а-а:а-а:а=а-2
а-а:а+а-а=а-1
а+а-а+а-а=а
аа:аа+а=1+а
а:а+а:а+а:а=2+а
.......... і так далі.

Зразок 2.
Створити алгоритм для складання чарівних числових стовпців Вінницького такого вигляду:
1 ... 2 ... 3 ...    ... 8 ... 9 = 0
1 ... 2 ... 3 ...     ... 8 ... 9 = 1
1 ... 2 ... 3 ...     ... 8 ... 9 = 2
1 ... 2 ... 3 ...     ... 8 ... 9 = 3
1 ... 2 ... 3 ...     ... 8 ... 9 = 4
................. і так далі

Де замість знаку ... можна нічого не ставити а дозволяється поставити будь-яку арифметичну дію: додавання, віднімання, множення, ділення. А також у виразі можна поставити: круглі дужки, квадратні дужки- це ціла частина від дробового числа, фігурні дужки - це дробова частина від будь-якого числа, можна поставити квадратний корінь, можна поставити дію факторіал числа.

Реалізація.

Покажимо алгоритми для окремого випадку n = 100. Тобто
1 ... 2 ... 3 ... ... 8 ... 9 = 100
Тоді отримаємо більше 10 варіантів:
1*2-3+4-5+6+7+89 =100
1+2+3+4+5+6+7+8*9 =100
(1+2+3-4)*5*6*(7+8):9=100
1+2+3-4+5+6+78+9=100
(1+2):3+4+5-6+7+89=100
1*2+34+56+7-8+9=100
12-3-4+5-6+7+89=100
123+45-67+8-9=100
123-4-5-6-7+8-9=100
123-45-67+89=100
123+4-5+67-89=100
12+3-4+5+67+8+9=100.

Зразок 3.
Створити алгоритм для складання магічного квадрату розміром 3х3 із довільних трьох різних чисел, які позначені латинськими змінними:
a, b, c. Умова магічності така. Треба щоб у кожному рядку таблиці стояли різні числа, у кожному стовпці таблиці стояли різні числа. А сума чисел кожного рядка дорівнювала добутку чисел кожного стовпця. А сума чисел кожного стовпця дорівнював добутку чисел кожного рядка.
Реалізація.
Розглянемо таке позначення адресу клітинки в числовій таблиці:
(1; 1)   (1; 2)   (1; 3)
(2; 1)   (2; 2)   (2; 3)
(3; 1)   (3; 2)   (3; 3)
Алгоритм матиме такі команди:
1. Число а поставити в такі комірки квадратної таблиці:
(1; 1)   (2; 3)   (3; 2)
2. Число b поставити в такі комірки квадратної таблиці:
(1; 2)   (2; 4)   (3; 3)
3. Число c поставити в такі комірки квадратної таблиці:
(1; 3)   (2; 2)   (3; 1)
Результат.
Утвориться такий квадрат на латинських
буквах.
a b c
b c a
c a b
Магічна сума дорівнює a + b+c =S
Магічний добуток дорівнює abc= P
Магічна сума і магічний добуток виконуються як по рядках, так і по стовпцях. Самостійно перевірте цю властивість для двох діагоналей створеного числового квадрата.
Питання, коли виконується умова
a+ b + c = abc, a=1; b=2; c=3.
1+2+3=1*2*3=6.
Отже, маємо гіпермагічний числовий квадрат 3х3 на сумах і на добутках:
1   2   3
2   3   1
3   1    2

Зразок 4.
Створити алгоритм для складання магічного квадрату розміром 4х4 із довільних чотирьох різних чисел, які позначені латинськими змінними:
a, b, c, d. Так щоб у кожному рядку таблиці були стояли різні числа, у кожному стовпці таблиці стояли різні числа.
Реалізація.
Розглянемо таке позначення адресу клітинки в числовій таблиці:
(1; 1)   (1; 2)   (1; 3)     (1; 4)
(2; 1)   (2; 2)   (2; 3)     (2; 4)
(3; 1)   (3; 2)   (3; 3)     (3; 4)
(4; 1)   (4; 2)   (4; 3)     (4; 4)
Алгоритм матиме такі команди:
1. Число а поставити в такі комірки квадратної таблиці:
(1; 1)   (2; 3)   (3; 4)     (4; 2)
2. Число b поставити в такі комірки квадратної таблиці:
(1; 2)   (2; 4)   (3; 3)     (4; 1)
3. Число c поставити в такі комірки квадратної таблиці:
(1; 3)   (2; 1)   (3; 2)     (4; 4)
4. Число d поставити в такі комірки квадратної таблиці:
(1; 4)   (2; 4)   (3; 1)     (4; 3) .
Результат.
Утвориться такий квадрат на латинських
буквах.
a b c d
c d a b
d c b a
b a d c
Магічна сума дорівнює a+b+c+d=S
Магічний добуток дорівнює abcd=P
Магічна сума і магічний добуток виконуються як по рядках, так і по стовпцях. Самостійно перевірте цю властивість для двох діагоналей створеного числового квадрата.

Зразок 5.
Створити алгоритм для складання магічного квадрату розміром 4х4 із 16 послідовних натуральних чисел, які позначені латинськими змінними:
a+1, а+2, а+3, ..., а+14, а+15, а+16. Так щоб у кожному рядку таблиці були стояли різні числа, у кожному стовпці таблиці стояли різні числа. Умова магічності така. Треба щоб сума чисел кожного рядка, сума чисел кожного стовпця, сума чисел головної і сума чисел бічної діагоналі дорівнювала числу, яке обчислюється за формулою:
М=(а+16)(а+17)/8.
Реалізація.
Розглянемо таке позначення адресу клітинки в числовій таблиці:
(1; 1)   (1; 2)   (1; 3)     (1; 4)
(2; 1)   (2; 2)   (2; 3)     (2; 4)
(3; 1)   (3; 2)   (3; 3)     (3; 4)
(4; 1)   (4; 2)   (4; 3)     (4; 4)
Алгоритм матиме такі команди:
1. Заповнюємо цей квадрат підряд, якщо а=0:
1     2     3    4
5     6     7    8
9    10   11 12
13   14   15   16
2. Переставляємо числа тільки на двох діагоналях за правилом. Відносно центру квадрата обмінюються місцями такі пари чисел: 1 і 16;   6 і 11; 7 і 10;   4 і 13.
3. Утвориться такий квадрат на магічний
квадрат на сумах. Якщо а=0:
16     2       3     13
5       11    10     8
9       7        6     12
4       14      15     1
Результат. Магічна сума квадрата 4х4 дорівнює 34.
Магічний добутку у цього квадрата відсутній.
Магічна сума 34 виконуються як по рядках, так і по стовпцях та двох діагоналях.

https://pythontask.pp.ua/

Практична частина

Завдання 1.

Створити і реалізувати алгоритм мовою програмування python3 для обчислення числових значень многочленів для дробових чисел і для цілих чисел.

Реалізація.

from math import fabs

import random

a= int(random.gauss(1, 8))+7

b =int(random.gauss(9, 14))+6

c=abs(int((a+b)*(a-b)-a**2+b**2+a/b)+8+b**2)

p= int(random.gauss(5, 10))+34

q= int(random.gauss(4, 9))+53

k= int(random.gauss(1, 8))+26

m=int(random.gauss(9, 14))+13

n=m%k+k%m+k//(m+1)+ p//(q+2)-k//(p+3)+m%p

print("a=",a, "b=",b,"Результат обчислення:c=", c, round(c, 4), type(c), bin(c))

print("p=",p, ";q=",q,";k=",k, ";m=",m,"Результат: n=", n, ";n^3=", pow(n,3))

print("Результат у 2-вій та 8-овій системі: n=", n,";n{2}=", bin(n), ";n{8}=",oct(n))

Протестувати цей алгоритм для таких значеннь змінних: 1)а=2.5 b=1.4; k= 3, m=2;

2) a=-1.25, b=-0.99, k=4, m=7. Для цього треба відмовитися від випадкових чисел в програмі!!!

Завдання 2.

Створити і реалізувати алгоритм мовою програмування python3 для нестандартного "символьного" обчислення числових значень виразів для дробових чисел і для цілих чисел з використанням функції еval.

Реалізація.

p="(5+6)**3-8*4+7/0.5"
t="78%3+96//7-4**3"
z="(9.8*7.6+5.4/3.2)**2"

w="a**2-b**3"
h="k**3+m**2"

a=float(input("Введіть дробове число а="))
b=float(input("Введіть дробове число b="))

c=(3*a+4*b)*(4*a-2*b)-a**3+b**3+a/(b-2)
k=int(input("Введіть ціле число k="))

m=int(input("Введіть ціле число m="))
n=m%k+k%m+k//m+ m//k-k**m+m**k

print("Результат обчислення c=", c, type(c))
print("Результат обчислення, n=", n, type(n))

print("Результат обчислення виразу p=", p+" =", eval(p), type(p))
print("Результат обчислення виразу t=",t+" =" , eval(t), type(t))

print("Результат обчислення виразу z=", z+" =", eval(z), type(z))
print("Результат обчислення виразу w=", w+" =", eval(w), type(w))

print("Результат обчислення виразу h=", h+" =", eval(h), type(h))

Протестувати цей алгоритм для таких значеннь змінних: 1)а=0.5 b=1.4; k= 7, m=9;

2) a=-2.75, b=-3.99, k=5, m=2.

Завдання 3.

Створити і реалізувати алгоритм мовою програмування python3 для обчислення побітових дій: ( &, ^, ~, >>, <<, |, ) з числaми.

Реалізація.

a=0

b=1

print("Побітові дії з числами:", " bin{a} = ", bin(a), " bin{b} = ", bin(b))

invers=(~a)

print("Це результат інверсій для числа a=", a, "invers=(~a)=", invers, type(invers))

print("Це результат інверсій числа в 2-овій системі: bin{~a} = ", bin(~a), " bin{~b} = ", bin(~b))

ampres=(a)&(b)

print("Це результат логічного and для двох чисел : ampres=", ampres, type(ampres))

logicor=(a)|(b)

print("Це результат логічного or для двох чисел: logicor=", logicor, type(logicor))

Протестувати цей алгоритм для таких значеннь змінних: 1)а=2 b=1; 2) a=5, b=3.

Завдання 4.

Створити і реалізувати алгоритм мовою програмування python3 для логічних операцій or, and, not з поняттями true та false.

Реалізація.

a=(input("Введіть логічне true або false для а="))
b=(input("Введіть логічне false aбо true для b="))
p=a or b

print("p=a or b=", p, type(p))
q=a and b

print("q=a and b=", q, type(q))
g= not b

print("g=not b =", g, type(g))
c=(a or b)and(not b)

k=(input("Введіть логічне false або true для k="))
m=(input("Введіть логічне true або false для m="))

n=(m and k) or (k or m) and (not k)
print("Результат (a or b)and(not b)=c=", c, type(c))
print("Результат (m and k) or (k or m) and (not k)= n=", n, type(n))

Протестувати цей алгоритм для таких значеннь змінних: 1)а=0 b=1; k= 1, m=1;

2) a=0, b=0, k=1, m=1.

Завдання 5.

Створити та реалізувати алгоритм мовою програмування Python3 для порівняння числових виразів за допомогою таких операцій порівняння: ==, >,<,<=,>=,!=, is, is not.

Реалізація.

from math import fabs

import random

x= abs(int(random.gauss(-5, -2)))

y=fabs(float(random.gauss(4.9, 7.8)))

print("логічний вираз ",x, ">", y, " має значення: ", x>y)

print("логічний вираз ",x, "<", y, " має значення: ", x<y)

print("логічний вираз ",x, ">=", y, " має значення: ", x>=y)

print("логічний вираз ",x, "==", y, " має значення: ", x==y)

print("логічний вираз ",x, "!=", y, " має значення:", x!=y)

Результат виконаної практичної роботи це файли( результатів виконання алгоритмів) надіслати вашому учителю на електронну скриньку:

vinnser@gmail.com (Сергій Петрович)

ktdfz@i.ua (Юрій Васильович)

Завдання для вироблення навичок програмування

Складіть програми мовою програмування або Scratch або Python або Pascal для розв´язування наступних задач

Найпростіші завдання з програмування

1.Програма задає два випадкових додатних парних числа k та b. Створити алгоритм мовою програмування, який спочатку додає до кожного числа однакове випадкове число, що більше 100, а потім знаходить потроєну суму двох чисел. А в остаточному результаті виводить остачу від ділення знайденої суми на 14.

2.Програма задає два випадкових непарних числа k та b, що більші, ніж 300 і менші 700. Створити алгоритм мовою програмування, який спочатку знаходить квадрати обох чисел, а потім середнє арифметичне цих квадратів. А в остаточному результаті виводить остачу від ділення середнього арифметичного на 11.

3.Програма задає два випадкових непарних числа k та b, що більші, ніж 540 і менші 980. Створити алгоритм мовою програмування, який спочатку знаходить більше число та його квадрат , а потім знаходить куб меншого числа, а потім знаходить їхнє середнє арифметичне квадрату та кубу. А в остаточному результаті виводить остачу від ділення середнього арифметичного на 12.

4.Програма задає два випадкових непарних числа k та b, що більші, ніж 135 і менші 700. Створити алгоритм мовою програмування, який спочатку знаходить більше число та його подвоює, а потім знаходить потроєне менше число, а потім знаходить їхнє середнє арифметичне. А в остаточному результаті виводить остачу від ділення середнього арифметичного на 17.

Довідник для учнів, що цікавляться програмуванням

Python

· Теорія

· I. Інтерпретатор Python

· Робота з редактором Python. Загальні питання. Інтерактивний та програмний режими роботи. Набір тексту програми

· II. Основи Python

· 1. Типи, числа, операції

· 1.1. Представлення даних в Python. Поняття об’єкту. Ідентичність, тип, значення об’єкту. Функції id(), type(). Оператори is, is not

· 1.2. Літерали. Створення (генерування) об’єкту. Базові типи об’єктів

· 1.3. Числа

· 1.3.1. Представлення чисел різних типів. Базові числові типи. Функції перетворення чисел

· 1.3.2. Числа з фіксованою точністю. Клас Decimal